What are Outliers?

In a very general way, outliers are outliers with respect to “something.” The discussions I have read about outliers seem to avoid dealing with the fact that there are two steps in outlier detection:

1. Defining what it means to be an outlier and then,
2. identifying the outliers.

Step 2 is easy. Step 1 is hard because it means one has to commit, not because it is technically difficult.

Can anyone define “outlier” in an absolute manner? beyond “a value that is highly unlikely given an assumed distribution.”

• What is the mental model behind stating that an observation is an outlier??

• Is there a single model for all situations? Probably not.

Because of these situations, Outliers can be very informative about the subject-area and data collection process. It’s essential to understand how outliers occur and whether they might happen again as a normal part of the process or study area.

Sometimes it’s best to keep outliers in the data. They can capture valuable information that is part of your study area. Retaining these points can be hard, particularly when it reduces statistical significance! However, excluding extreme values solely due to their extremeness can distort the results by removing information about the variability inherent in the study area. You’re forcing the subject area to appear less variable than it is in reality.

Unfortunately, resisting the temptation to remove outliers inappropriately can be difficult. Outliers increase the variability in your data, which decreases statistical power.

Consequently, excluding outliers can cause your results to become statistically significant.

When considering whether to remove an outlier, you’ll need to evaluate if it appropriately reflects your target population, subject-area, research question, and research methodology.

Causes for Outliers

In broad strokes, there are three causes for outliers: - data entry (human errors) or measurement errors (instrument errors), - sampling problems and unusual conditions, and - natural variation (not an error, novelties in data)

Types of Outliers

Outliers can be of two kinds: univariate and multivariate.

• Univariate outliers can be found when looking at a distribution of values in a single feature space.

• Multivariate outliers can be found in a n-dimensional space (of n-features). Looking at distributions in n-dimensional spaces can be very difficult for the human brain, that is why we need to train a model to do it for us.

Outliers can also come in different flavours, depending on the environment: point outliers, contextual outliers, or collective outliers.

• Point outliers are single data points that lay far from the rest of the distribution.

• Contextual outliers can be noise in data, such as punctuation symbols when realizing text analysis or background noise signal when doing speech recognition.

• Collective outliers can be subsets of novelties in data such as a signal that may indicate the discovery of new phenomena (As in figure B).

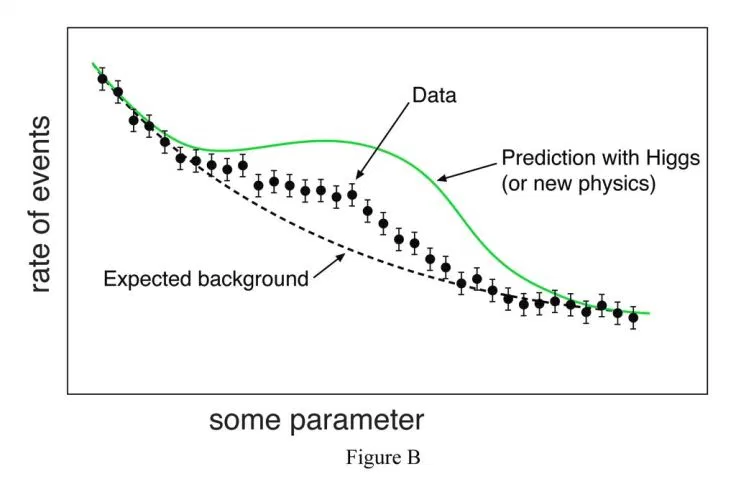
Philosophy about Finding Outliers

Outlier detection methods have been suggested for numerous applications, such as credit card fraud detection, clinical trials, voting irregularity analysis,data cleansing, network intrusion, severe weather prediction, geographic information systems, athlete performance analysis, and other data-mining tasks.

As you saw, there are many ways to identify outliers. The philosophy is that you must use your in-depth knowledge about all the variables when analyzing data. Part of this knowledge is knowing what values are typical, unusual, and impossible.

When you have this in-depth knowledge, it’s best to use the more straightforward, visual methods.

At a glance, data points that are potential outliers will pop out under your knowledgeable gaze. Consequently, I’ll often use boxplots, histograms, and old-fashioned data sorting These simple tools provide enough information to find unusual data points for further investigation.

Typically, I don’t highly recommend Z-scores and hypothesis tests to find outliers because of their various complications. But I will introduce a couple of hypothesis tests to detect outliers in the later posts.

As you already know, using outlier tests can be challenging because they usually assume your data:

1. follow the normal distribution, and then
2. there might be possible masking and swamping.

Additionally, the existence of outliers makes Z-scores less extreme. It’s ironic, but these methods for identifying outliers are actually sensitive to the presence of outliers! Fortunately, as long as researchers use a simple method to display unusual values, a knowledgeable analyst is likely to know which values need further investigation.

In my view, the more formal statistical tests and calculations are overkill because they can’t definitively identify outliers. Ultimately, analysts must investigate unusual values and use their expertise to determine whether they are legitimate data points. Statistical procedures don’t know the subject matter or the data collection process and can’t make the final determination. You should not include or exclude an observation based entirely on the results of a hypothesis test or statistical measure.

At this stage of the analysis, we’re only identifying potential outliers for further investigation. It’s just the first step in handling them. If we make errors, we want the errors on the side of investigating too many values rather than too few.

General Rules

• Not all outliers are bad and some should not be deleted. In fact, outliers can be very informative about the subject-area and data collection process. It’s important to understand how outliers occur and whether they might happen again as a normal part of the process or study area. If you could keep them (so-called outliers here) in your data, it’s the best.

  • Another approach is to perform the analysis with and without these observations and discuss the differences. Comparing results in this manner is particularly useful when you’re unsure about removing an outlier and when there is substantial disagreement within a group over this question.

• When you decide to remove outliers, document the excluded data points and explain your reasoning. You must be able to attribute a specific cause for removing outliers.

– To be Continued